科普王国展品介绍(一)——数学展区
展馆介绍
“科普王国”展厅位于少儿科技馆二层,建筑面积3808平方米,属于基础学科展厅,展出的是一些经典的基础学科项目。其中,展品包括力学、光学、声学、电磁学及数学等学科的科普项目70余个。本馆项目需要少年儿童的参与和互动,通过体验,少年儿童不仅可观察到一些在课堂上看不到的科学现象,而且加深对书本知识的理解和深入思考,从而探索科学的兴趣得到很大的激发。
本馆代表性的项目有:1.著名科学家塑像群;2.磁悬浮地球仪;3.声音的舞蹈;4.钉床;5.电磁发电机;6.数学曲线;7.电磁火箭;8.可以省力的滑轮;9.风力发电;10.太阳能喷泉;11.太阳能发电组合等七十多个项目。

科普王国”展厅部分展品展项
1.数学展区
(1)方轮子

互动方式:
本展项由一只方轮子和一段曲率、弧长均相等的弧形“路面”组成。游客可以操作方形轮子,让它在“路面”上滚动,发现轮子的轴心却始终在同一平面上移动。
原理:
其实,方轮子轨道是一种倒悬链线,它因形状与两端固定而中间下坠的绳子相似而得名。为方便理解,可这样思考:截取一段完整的弧状凸起,粘贴到方轮子的任意一条边上,再将方轮子的其他三边重复上述操作,方轮子就变成普通的圆轮子了,所以方轮子的轴心能够在同一平面上移动。这体现了曲线与方轮之间的数学关系。
(2)分形艺术

互动方式:
游客可以欣赏灯箱上美妙的分形图案,并可以通过计算机绘制分形图像,制作自己的分形图案。
原理:
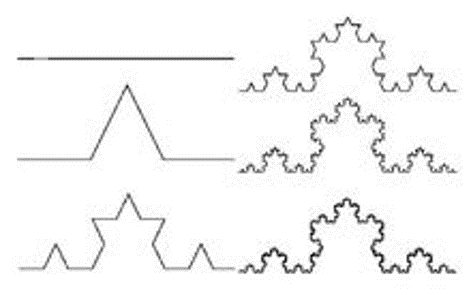
分形最基本的含义为:许多事物和现象在形状、结构、性质、功能等方面具有精细层次,且在不同层次上具有某种意义上的相似性质。分形几何的最重要、最直接的应用领域是计算机图形学,它为自然景物的模拟提供理论基础及造型方法。
分形艺术作品具有以下基本特征:一、自相似性;二、无限精细; 三、极不规则。分形图案的制作过程大致如下:
(3)勾股定理
互动方式:
转盘上有三个装有蓝色液体的透明框,框都是正方形的。 游客转动转轮就会发现大方框内液体刚好可以充满中方框和小方框,其中隐喻的就是勾股定理a²+b²=c²,a、b、c分别是小中大三方框的边长。
原理: 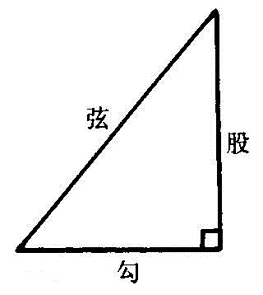
早在公元前11世纪的西周初期,数学家商高曾与辅佐周成王的周公谈到直角三角形具有这样的一个性质:如果直角三角形的两个直角边分别为3和4,则这个直角三角形的斜边为5。
利用商
(4)数学小游戏
隐形小精灵
隐形小精灵是由三块木板拼成的一幅画,上面画有13个圣诞老人,如果将三块木板中上面的两块对调后,圣诞老人的个数就只有12个了。


八皇后

八皇后问题是一个古老而著名的命题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯提出:在一个8×8的棋盘上(国际象棋)按规则摆放八枚皇后棋子,要求:
A.同一横行只能摆放一粒皇后棋子;
B.同一纵列只能摆放一粒皇后棋子;
C.同一斜线上只能摆放一粒皇后棋子。高斯认为有76种方案。后来有人用图论的方法解出92种结果。
汉诺塔

互动方式:
汉诺塔的游戏要求是将左边柱子上按顺序摆放的圆盘全部移到右边的柱子上,并且依然按照从上到下由小到大的顺序摆放。在移动圆盘的同时遵守规则:
1.每次只能移动一只圆盘;
2.任何时刻都不能出现大圆盘摞在小圆盘上的情况;
3.在移动圆盘的过程中可以利用中间的石柱作为过渡,但仍需遵守规则1和2。
原理:
当有n块圆盘的时候,需要移动多少次才能完成汉诺塔要求的操作呢?当n=1时,需要移动的次数为f(1)=1=21-1;当n=2时,需要移动的次数为f(2)=3=22-1;当n=3时,需要移动的次数为f(3)=7=23-1;以此不难证明有n个盘时需要的移动次数为f(n)=2n-1。
(5)双曲狭缝

互动方式:
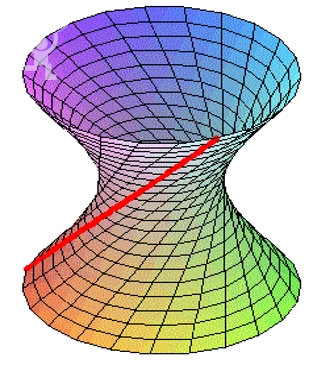
该展品展示了由一根倾斜的直线旋转形成的一个二次曲面的轨迹。你可以拨动展品的金属圆棒,当金属棒旋转起来以后,可观察到金属棒的运动轨迹,从而了解了有关二次曲面的简单知识。
原理:
双曲狭缝一根倾斜的直棍绕 Z 轴旋转时,其产生的双曲面(如下图所示)被 X-Y 平面切割留下的图形。直棒能巧妙地穿越它,是因为直棍转动时会在空中划出一种被称为双曲面的立体图形,从双曲线的顶端到底部沿弯曲的边缘划出的线称为双曲线,透明板上所刻的曲线就是双曲线,而且也正好与直棒所划出的双曲线相符,所以它可以顺利通过平板上的双曲狭缝。
(6)数学曲面

互动方式:
你可以亲自操作计算机,从中了解各种曲面知识。游客可以逐个地观察各个不同的曲面,去分辨他们在数学上属于哪一种类型的曲面,可以尝试以数学的方式去描述这个曲面,比如:双曲面、球面等。
原理:
曲面是一条动线,在给定的条件下,在空间连续运动的轨迹。数学曲面是数学原理及规律的图形描述,广义上说物体的表面都可以用或近似用数学曲面描述。我们根据形成曲面的母线形状我们可以将曲面可分为直线面(由直线运动而形成的曲面)和曲线面(由曲母线运动而形成的曲面)。曲面是我们生活中最常见的二维物体或三维空间结构,了解曲面有助于我们改善我们的生活、发现生活中的新事物,有助于我们学习自然科学知识。
(7)麦比乌斯带

互动方式:
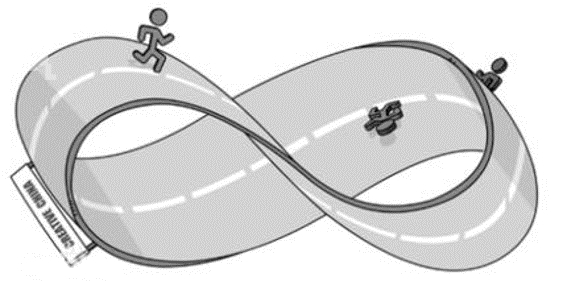
细看展品你会发现,展品的两面是连续的,此种连续不存在跨越或奇点的(即是大的空间曲率或者可以理解为折点)。
原理:
本模型是德国数学家麦比乌斯提出的数学模型。它是由一个截面为三角形的特殊构造多次旋转而成。你可以用展台上的工具亲自做做看:先用剪刀裁出一条细长的纸,然后把它拧180度再粘上,你就会得到一个麦比乌斯带,而且会发现当你用手指把一面整个走了一遍以后,就走到了另外一面,而继续走下去,又会回到开始的一面。
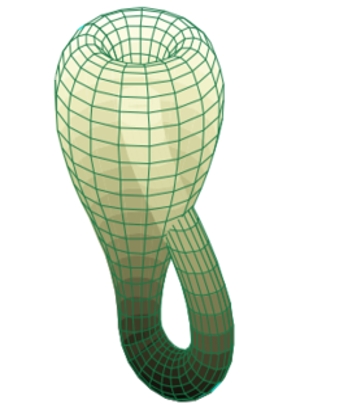
(8)克莱因瓶
互动方式:
玻璃罩内的玻璃制品就是克莱因瓶,仔细看就会发现,克莱因瓶与麦比乌斯带一样,内外两面是连续的,而且此连续式不存在跨越和奇点的。
原理:
“克莱因瓶”是一个经典的特殊曲面构造即一个真正的闭合曲面,但是却没有所谓的“内外”之分。该瓶展示的是一种四维构造,并且当你把该瓶直截之后展开,你会发现,它们是两条麦比乌斯带。该展品能帮助游客建立起初步的四维空间基础概念,激发游客的想象力与探索自然科学的热情。
(9)杰出数学家


祖冲之(Zu Chong Zhi,公元429—500年 南北朝时代)现河北省涞源县人。他通晓数学、天文历法、机械制造、音乐、文学。他在数学方面的成就尤为突出,计算出圆周率在3.1415926—3.1415927之间,成为世界上最早把圆周率推算到七位数字以上的科学家。此外他在天文历法和机械制造方面也颇有造诣,不仅创制“大明历”,还制造出指南车、“千里船”和“水碓磨”。

华罗庚(Hua Luo Geng,1910—1985)江苏金坛人,中国科学院院士。他主要从事解析数论、矩阵几何学、典型群、自守函数论、多复变函数论、偏微分方程、高维数值积分等领域的研究与教授工作并取得突出成就。并倡导应用数学与计算机的研制,曾出版《统筹方法平话》、《优选学》等多部著作并在中国推广应用。
他在40年代,解决了高斯完整三角和的估算这一历史难题,得到了最佳误差阶估计(此结果在数论中有着广泛的应用)。另外对G.H.哈代与J.E.李特尔伍德关于华林问题及E.赖特关于塔里问题的结果作了重大的改进,至今仍是最佳记录。

陈景润(Chen Jing Run,1933—1996)福建省福州市人,中国现代数学家,世界著名解析数论学家之一。1953年毕业于厦门大学数学系。他对一系列数学问题进行了深入研究,并取得了卓越成就。其中攻克世界著名数学难题“哥德巴赫猜想”中的(1+2)问题最为著名,创造了距摘取这颗数论皇冠上的明珠(1+1)只是一步之遥的辉煌。



